Winning the CHSH game with Cirq and Bayesian Optimization
Trying to violate the Bell Inequality.
Table of Contents
Introduction
In this post we’ll be going through a simple experiment I’ve set up in order to violate the Bell inequality.
The goal is to “win” (one of the formulations of) the CHSH game: this “game” was proposed by Clauser, Horn, Shimony and Holt in their famous 1969 PRL paper 1 as a generalizatio of 1964 Bell’s Theorem. The formulation we’ll be dealing with is the one proposed by Mark Wilde in his book 2 and by Ronald de Wolf in his lecture notes 3.
You can find the code here.
Description of the game
Here’s the game description by Mark Wilde:
This game is a 2-player game where the two players, Alice and Bob, are spatially separated from each other from the time that the game starts until it is over. The game begins with a referee selecting two bits $x$ and $y$ uniformly at random. The referee then sends $x$ to Alice and $y$ to Bob. Alice and Bob are not allowed to communicate with each other in any way at this point. Alice sends back to the referee a bit $a$, and Bob sends back a bit $b$. Since they are spatially separated, Alice’s response bit $a$ cannot depend on Bob’s input bit $y$, and similarly, Bob’s response bit $b$ cannot depend on Alice’s input bit $x$. After receiving the response bits $a$ and $b$, the referee determines if the AND of $x$ and $y$ is equal to the exclusive OR of $a$ and $b$. If so, then Alice and Bob win the game.
Given that, the winning conditions is
$$ x \land y = a \oplus b $$
Deterministic strategy
A deterministic strategy would have Alice select a bit $a_x$ conditioned on the bit $x$ that she receives, and similarly, Bob would select a bit $b_y$ conditioned on $y$. The following table presents the winning conditions for the four different values of $x$ and $y$ with this deterministic strategy:
| $x$ | $y$ | $x \land y$ | $a_x \oplus b_y$ |
|---|---|---|---|
| 0 | 0 | 0 | $a_0 \oplus b_0$ |
| 0 | 1 | 0 | $a_0 \oplus b_1$ |
| 1 | 0 | 0 | $a_1 \oplus b_0$ |
| 1 | 1 | 1 | $a_1 \oplus b_1$ |
At most, only three out of four of them can be satisfied, so that the maximal winning probability with a classical deterministic strategy is at most $3 / 4$. We can then see that a strategy for them to achieve this upper bound is for Alice and Bob always to return $a = 0$ and $b = 0$ no matter the values of $x$ and $y$.
Quantum strategy
Now consider the same problem but where Alice and Bob are supplied with a shared 2-qubit system initialized to the entangled state
$$ \frac{1}{\sqrt{2}} (|00\rangle - |11\rangle) $$
The strategy is the following: if $x = 0$ then Alice applies $R(-\pi/16)$ to her qubit and if $x = 1$ she applies $R(3\pi/16)$, where $R(\theta)$ denotes a rotation of $\theta$:
$$ R(\theta) = \begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & \cos(\theta) \end{bmatrix} $$
Bob’s procedure is the same, depending on his input bit $y$.
If Alice now rotates her qubit by $\theta_A$ and Bob rotates his qubit by $\theta_B$ then the state becomes:
$$ \frac{1}{\sqrt{2}} (cos(\theta_A + \theta_B))(|00\rangle - |11\rangle) + \sin(\theta_A + \theta_B)(|01\rangle + |10\rangle) $$
Measuring in the computational basis we see that, after the measurements, the probability that $a \oplus b = 0$ is $cos(\theta_A + \theta_B)^2$. If $x \land y = 0$ then $\theta_A + \theta_B = \pm \pi / 8$, else if $x \land y = 1$ then $\theta_A + \theta_B = 3 \pi / 8$.
The winning condition is then satisfied with probability $cos(\pi / 8)^2 \approx 0.853$, for all four input possibilities, showing that quantum entanglement allows Alice and Bob to win the game with a probability that’s higher than what the best classical strategy can achieve. Tsirelson 5 showed that $cos(\pi / 8)^2$ is the best that quantum strategies can do for CHSH, even if they are allowed to use much more entanglement than one Bell state.
Winning at the game without designing a winning strategy
Quantum computing (QC) is one of the currently “hot” research areas, gaining substantious advantages year after year. Many industries and Universities are developing interesting tools for experimenting with the power of QC, such as IBM’s qiskit and Google’s cirq.
These two examples are Python-based frameworks for programming quantum computers and, in this experiment, I used Cirq. My idea is simple: I wanted to construct a parameterized quantum circuit (PQC) that, along with an optimization strategy, could find the best parameters for winning at the CHSH game.
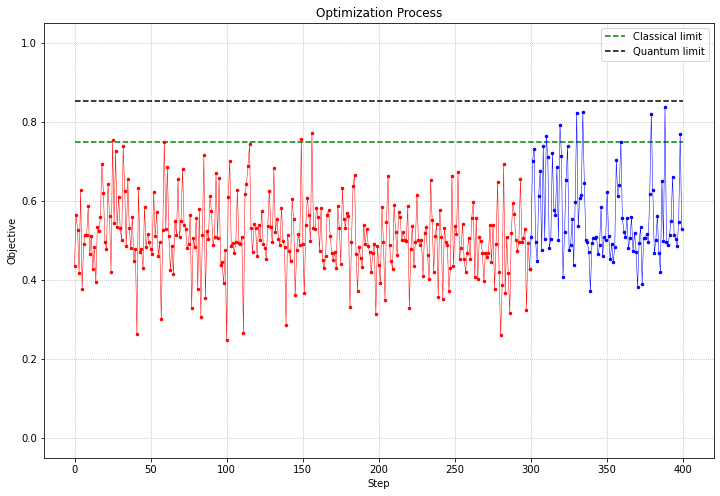
The optimization strategy I employed is Bayesian Optimization, which is a strategy for global optimization of black-box functions. Bayesian optimization is particularly advantageous for problems where the function we want to maximize is difficult to evaluate, is a black box with some known structure, relies upon less than 20 dimensions, and where derivatives are not evaluated 4.
Turns out this is exactly my setting, since I want to maximize the probability of winning the CHSH game through a series of simulations of a few-parameterized-gates quantum circuit. The circuit I designed is the following
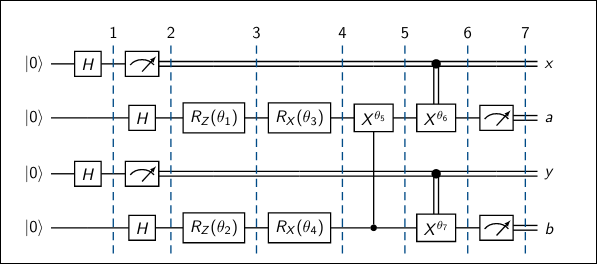
where the four qubits are initialized to $|0\rangle$. The transformations which operate on these qubits are Hadamard gates (denoted by $H$), rotations $R_X$ and $R_Z$ (respectively by the $X$ and $Z$ axis) and CNOTs. Rotations and controlled-not gates are parameterized by the $x*$ you see in the pictures: I’ve constrained the rotational parameters into $[0, 2\pi]$ and the exponents of the CNOTs to $[-2, 2]$. The last *moment* of the circuit is the one dedicated to Measurements, which happen in the computational basis.
For every set of fixed parameters a simulation of $N=1000$ runs is operated and, in the end, a winning statistic is calculated as $N^w / N \in [0, 1]$, where $N^w$ is the number of times that the winning condition is satisfied. This function is then maximized through Bayesian Optimization resulting in a set of parameters which are able to win the game: